W jednym z wpisów sprzed kilku miesięcy opisywałem, jak wyliczać ścieżkę krytyczną w projekcie. Jednak ostatnia wysoka popularność tego wpisu oraz jego powtórna lektura sprowokowały mnie do wniosku, że chyba nie dostatecznie rozdrobniłem algorytm wyliczania zapasów swobodnych, a potrzeby czytelników rosną. Zatem jeszcze raz, jak to się robi w spowolnionym tempie.
Zagraj w naszą grę online, która w czasie rzeczywistym pokazuje jak wpływa ścieżka krytyczna na projekt – kliknij tutaj.
Załóżmy, że mamy zestaw zadań powiązanych ze sobą jak poniżej:
| Zadanie | Poprzednik | Czas trwania, np. dni |
| A | brak | 2 |
| B | A | 5 |
| C | A | 4 |
| D | B | 3 |
| E | D, C | 2 |
| F | E | 3 |
| G | B, E, F | 1 |
| H | G | 5 |
Dla uproszczenia w omawianym przykładzie mamy do czynienia z zależnościami typu Finish-Start (po polsku Zakończenie do Rozpoczęcia), więcej o typach zależności można przeczytać w poprzednim wpisie na temat ścieżki krytycznej.
Maciupci krok 1. Narysujmy diagram sieciowy
A jest pierwszym zadaniem, bo nie ma żadnych poprzedników. Gdyby zadań bez poprzedników było więcej, wówczas trzeba dodać wirtualne zadanie startowe, które ma czas trwania równy 0.
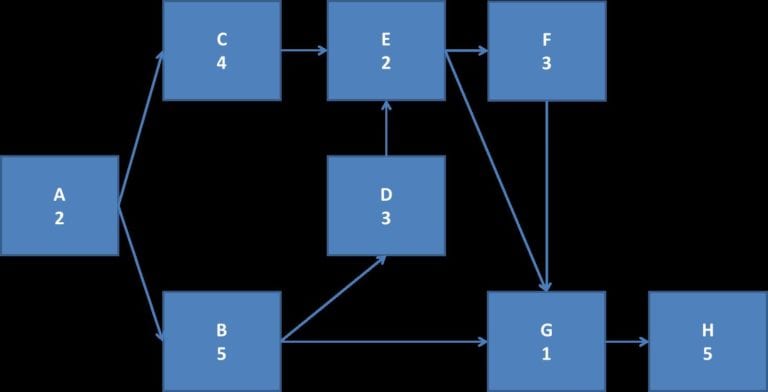
Powinien wyjść nam mniej więcej taki, jak na rysunku. Pod symbolami zadań umieściłem ich czasy trwania.
Jak widać ostatnie zadanie, to H. Gdyby się okazało, że końcowych zadań jest więcej niż jedno, również trzeba by dodać wirtualne zadania końcowe o czasie trwania 0.
Naprawdę niewielki krok 2. Marsz do przodu
W górnym rogu każdego zadania wpisujemy najwcześniejszy możliwy czas rozpoczęcia i zakończenia.
- I tak dla A wynosi on 0, bo można od razu zacząć.
- Natomiast jego najwcześniejszy czas końca to 2, bo jego czas trwania + 0 = 2. Idąc dalej B może najwcześniej rozpocząć się w drugim 2 dniu i zakończyć w 7 dni, bo 2 + 5 = 7.
- Analogicznie C może najwcześniej zacząć się w 2 dniu i skończyć w 6.
- D zacznie się w …. 7 i skończy w 10.
- Zaś E zależy od dwóch zadań, zadań idąc po ścieżce A->C->E może zacząć się w 6 dniu. Natomiast po ścieżce A->B->D->E może zacząć się w 10 dniu. Zatem E najwcześniej może zacząć się w 10 dniu, bowiem trzeba uwzględnić wszystkie zależności. E skończy się więc w 12 dniu.
- F to proste: 12 / 15.
- Analogicznie do E, zadanie G zależy od trzech zadań: po ścieżce A->B->G: 7 / 8; po ścieżce A->C->E->G: 12 / 13; a po ścieżce A->C->E->F->G: 15 / 16. Uwzględniwszy wszystkie trzy zależności okazuje się, że najwcześniej G zacznie się 15 dnia i skończy 16.
- H już z górki: 16 / 21.
Zatem już wiadomo, że projekt będzie trwał 21 dni. Poniżej odpowiednio zaktualizowany rysunek diagramu sieciowego.
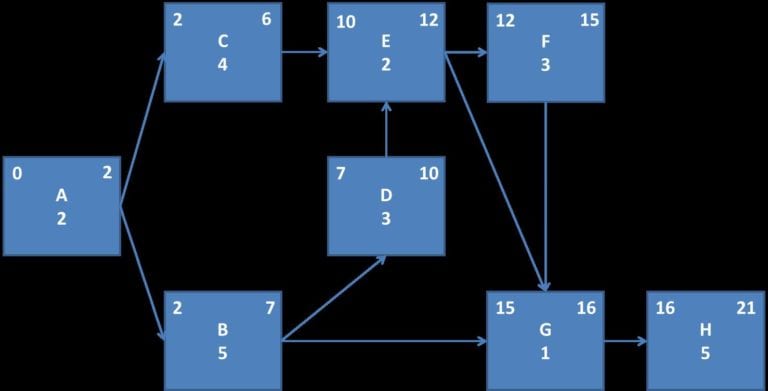
Ostatni tyci krok 3. Powrót
Teraz należy udać się dołem narysowanych kwadratów od ostatniego z nich, czyli H, aby wyliczyć najpóźniejsze czasy startów i końców zadań.
- H skończy się najpóźniej 21 dnia i zacznie 16, bo jego czas trwania to 5 dni.
- G odpowiednio: 16 / 15.
- F analogicznie: 15 / 12.
- E ma dwa zadania będące jego następnikami, zatem jego najpóźniejsze zakończenie zależy od obu tych zadań. I tak po sekwencji H<-G<-E skończy się najpóźniej 15 dnia, a po sekwencji H<-G<-F<-E: 12 dnia. Zatem, aby uwzględnić obie te zależności należy przyjąć mniejszą, czyli 12 dni. Toteż E najpóźniej zacznie się 10 dnia.
- D odpowiednio: 10 / 7.
- C odpowiednio: 10 / 6.
- Zaś B, mając dwa następniki najpóźniej skończy się 7 dnia, a zacznie 2.
- W końcu A też posiadające dwa następniki najpóźniej skończy się 2 dnia.
Obrazuje to poniższy rysunek.
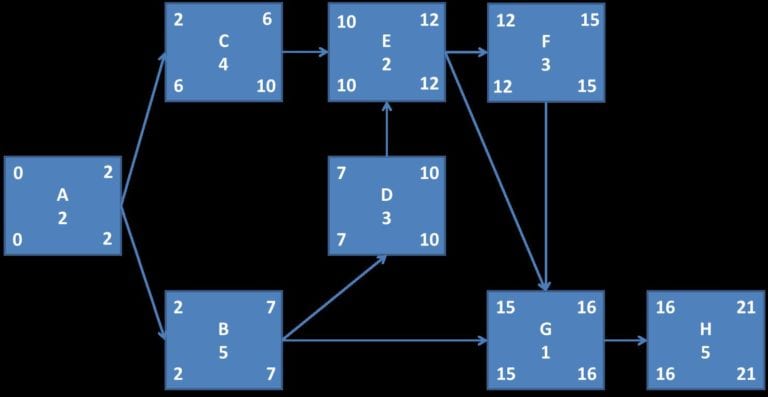
Naprawdę ostatni krok 4. Wyznaczenie zadań krytycznych
Teraz wystarczy pokolorować na czerwono zadania, dla których czasy najwcześniejsze równają się najpóźniejszym, to jest nasza ścieżka krytyczna. Pozostałe z nich, w tym przykładzie zadanie C, mają zapas, czyli czas, o który mogą się opóźnić bez wpływu na cały projekt. Patrz rysunek poniżej.
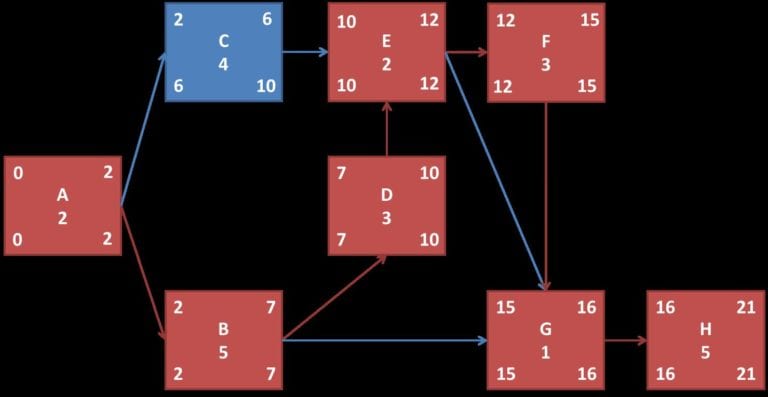
To wszystko, łatwiej już nie umiem tego wytłumaczyć.
Ps.
Tytuł został zaproponowany przez moją żonę i tak musi zostać.










Bez przesady. Narysujesz Ganta i te starożytne wyliczenia nie mają sensu.
Sposób, przyznam, miły. Ale niepotrzebny.
Tak, wiem. Gantta. A nie Ganta.
Zgadzam się, natomiast, jak już wspominałem w poprzednim wpisie na ten temat, ta umiejętność jest potrzebna, aby zdać egzamin na studiach lub certyfikacyjny.
Natomiast rysowanie Gantta to nic innego jak tworzenie diagramu sieciowego właśnie, resztę kroków faktycznie zrobi program taki, jak MS Project.
A przed sesją naprawdę wielu ludzi szuka takich informacji 🙂
Ups. Nie przeczytałem poprzedniego artykułu. My bad. Na egzaminie rzeczywiście trzeba wyliczać 🙂
Dobrze wytłumaczony temat. Zawsze można wrócić i sobie powtórzyć. 🙂
Rozpoczęłam w tym tygodniu cykl szkolem z PM. Nie mam doświadczenia niemal żadnego, nie jestem po zarządzaniu. Po dzisiejszym wykładzie i warsztatach z harmonogramowania załamałam się na ścieżce krytycznej. Bylam gotował strzelić sobie w mózg bo nie zrozumiałam. DZIĘKI Ten maciupciokroczkowy tekst pomógł rozjaśnił dopełnił .
🙂